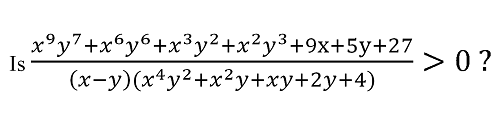by our Quantitative Reasoning Faculty
In last time’s blog we looked at why DS is so important in GMAT. In this one we’ll take a look at the 3 key things that you need to do in order to tackle this unfamiliar question type. There are:
1. Learn the Options
The first step in learning DS is to get absolutely familiar with the options. Fortunately, in DS, this is easy because the five options are always as follows:

(A) Statement (1) alone is sufficient but statement (2) alone is not sufficient to answer the question asked
(B) Statement (2) alone is sufficient but statement (1) alone is not sufficient to answer the question asked
(C) Both statements (1) and (2) together are sufficient to answer the question asked, but neither statement alone is sufficient
(D) Each statement alone is sufficient to answer the question asked
(E) Statements (1) and (2) together are not sufficient to answer the question asked and additional data are needed.
2. Remember the Aim
Remember, in DS our aim is NOT TO FIND THE FINAL ANSWER to the question but just to verify whether the INFORMATION GIVEN IN THE TWO STATEMENTS IS SUFFICIENT TO REACH TO THE FINAL ANSWER!
So while solving the question if, at any intermediate step, you realize that you can reach the final answer then QUIT and mark the option accordingly.
3. Understand the Approach
Now let’s have a look at how you should approach DS questions.
Step 1: Carefully Read the Question Statement and Find the Crux of the Question
After closely examining the question statement and before you read the information given in statements (1) and (2), ‘identify the crux of the question’. What I mean by ‘the crux of the question’ is the piece of information that is the key to the solution. Sometimes you have to think a little bit before you get it. But once you have it, it will lead you straight to the answer. For example, have a look at this question statement:
If x and y are distinct positive integers then:
(1) x = 2 (y + 3)
(2) x2 = y2 + 4
Now, if you have lost touch with maths, just the sight of that forest of terms is enough to want to make you give up. But again, remember that we are not at all interested in solving this inequality. We just need find out whether the expression on the left hand side is positive or not (that’s what is implied by >0) – and this is a much simpler matter! Further, in this mass of algebraic symbols is a key that reveals itself when you examine about the expression and think about it a little.
In order to get this key, the first thing to do is to carefully observe the question statement. First and foremost, it says, that x and y are distinct positive integers. This is a very important piece of information – and you’ll understand why in a moment. Secondly, if you observe the numerator of the expression on the left, it consists of additions throughout. Given both these pieces of information, the numerator has to be positive in nature: it is the sum of distinct positive integers (which is why the information about x and y was important). By the same logic, even the second bracket in the denominator has to be positive. The only unknown factor, therefore, is the first bracket in the denominator, i.e., (x – y) and this is what holds the key to the entire problem.
The entire expression will be positive if and only if (x – y) > 0, in short, if x > y. On the other hand, if x < y, the whole expression will be negative. So, the whole gigantic problem is reduced to an extremely simple question: is x > y? Once we have arrived at this conclusion, cracking the rest of the problem is really easy: any information about the relative magnitudes of x and y will be sufficient to arrive at the answer! Thus, in this case, the crux of the question (the key to the solution) is realizing that all we need to find out in order to answer this question is whether statements (1) and (2) allow us to decide whether x is bigger than y or vice versa.
Once you have reached this stage you are can confidently take on the options of this seemingly insoluble problem. The discussion above takes care of Step 1 of the approach i.e. carefully reading the question statement and finding the crux of the question. In the next post we’ll look at Step 2 of the approach: tackling the options in DS questions – and we’ll be giving you tips that will reduce the complexities to a few simple steps! Watch for the tips in our third DS blog post next week.